797. 所有可能的路径 - 已题解语言：Python/Java/C++/JavaScript/C#/Go/Ruby

LeetCode Python, Java, C++ > 图论 > 797. 所有可能的路径 > 已支持 Python, Java, C++, JavaScript, C#, Go, Ruby > LeetCode GitHub Code 或转发

力扣链接：797. 所有可能的路径，难度等级：中等。

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j] 存在一条有向边）。

示例 1:

输入: graph = [[1,2],[3],[3],[]]

输出: [[0,1,3],[0,2,3]]

解释: 有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2:

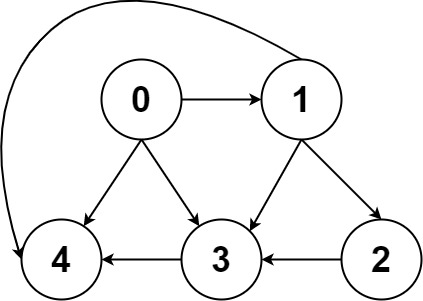
输入: graph = [[4,3,1],[3,2,4],[3],[4],[]]

输出: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

约束:

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素 互不相同
保证输入为 有向无环图（DAG）

思路
上一题 下一题

“深度优先搜索”的模式

深度优先搜索（DFS）是一种经典的图遍历算法，其核心特点是“尽可能深”地探索图的分支。DFS 从起始顶点出发，沿着一条路径不断深入，直到到达没有未访问邻接点的顶点，然后回溯到最近的分叉点继续探索。这一过程通过递归或显式栈（迭代法）实现，形成“后进先出”的搜索顺序，因此 DFS 在非加权图中能快速找到离起点较远的深层节点。

与 BFS 的对比：

搜索顺序：DFS 优先探索深度方向，而广度优先搜索（BFS）按层逐层扩展，形成“先进先出”的队列结构。
适用场景：DFS 更适合强连通分量或回溯类问题（如迷宫所有路径），而 BFS 擅长最短路径（未加权图）或邻近节点探索（如社交网络好友推荐）。

DFS 的独特性：

不完全性：若图无限深或存在环路（未标记已访问），DFS 可能无法终止，而 BFS 总能找到最短路径（未加权图）。
“一支笔走到底” 的搜索风格，使其在回溯剪枝或记录路径时更具灵活性，但也可能错过近邻最优解。

总之，DFS 以深度优先的策略揭示图的纵向结构，其回溯特性与栈的天然结合，使其在路径记录和状态空间探索中表现突出，但需注意处理环路和最优解缺失的局限性。

步骤

初始化一个空列表 paths，用于存储所有找到的有效路径。
初始化一个堆栈来管理 DFS 遍历。堆栈中的每个元素将存储一个 pair（或元组），其中包含当前 node 和到达该节点所采用的 path。
将起始状态加入到堆栈：初始节点 0 和一个空的路径列表（例如 (0, [])）。
当堆栈不为空时：
- 从堆栈中弹出顶部元素，检索当前 node 及其关联的 path。
- 通过将当前 node 附加到从堆栈中弹出的 path 来创建一个 currentPath 数组，它表示通往当前节点并包含当前节点的路径。
- 检查当前 node 是否为目标节点（n - 1，其中 n 是节点总数）。
  - 如果它是目标节点，则将 currentPath 添加到 paths 数组中，因为已经找到了从源节点到目标节点的完整路径。
  - 如果不是目标节点，则遍历当前 node 可访问的所有 neighbor 节点（即遍历 graph[node]）。
    - 对于每个 neighbor，将一个新的 pair（neighbor 节点和 currentPath）加入到堆栈中。这为遍历探索从邻居节点延伸的路径做好准备。
循环结束后（堆栈为空），返回 paths 数组，其中包含从节点 0 到节点 n - 1 的所有已发现路径。

复杂度

时间复杂度

Too complex

空间复杂度

Too complex

Python #

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        paths = []
        stack = [(0, [])]

        while stack:
            node, path = stack.pop()

            if node == len(graph) - 1:
                paths.append(path + [node])
                continue

            for target_node in graph[node]:
                stack.append((target_node, path + [node]))

        return paths

Java #

class Solution {
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        List<List<Integer>> paths = new ArrayList<>();
        // Each element in the stack is a pair: (current_node, current_path)
        Stack<Pair<Integer, List<Integer>>> stack = new Stack<>();
        List<Integer> initialPath = new ArrayList<>();
        stack.push(new Pair<>(0, initialPath));

        int targetNode = graph.length - 1;

        while (!stack.isEmpty()) {
            var current = stack.pop();
            int node = current.getKey();
            var path = current.getValue();

            var nextPath = new ArrayList<>(path);
            nextPath.add(node);

            if (node == targetNode) {
                paths.add(nextPath);
                continue;
            }

            for (int neighbor : graph[node]) {
                stack.push(new Pair<>(neighbor, nextPath));
            }
        }

        return paths;
    }
}

C++ #

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        vector<vector<int>> paths;
        // Stack stores pairs of (current_node, current_path)
        stack<pair<int, vector<int>>> s;
        s.push({0, {}}); // Start at node 0 with an empty path initially

        int targetNode = graph.size() - 1;

        while (!s.empty()) {
            auto node_path = s.top();
            s.pop();
            int node = node_path.first;
            vector<int> path = node_path.second;

            // Add the current node to the path
            path.push_back(node);

            if (node == targetNode) {
                paths.push_back(path); // Found a path to the target
                continue;
            }

            // Explore neighbors
            for (int neighbor : graph[node]) {
                s.push({neighbor, path});
            }
        }

        return paths;
    }
};

JavaScript #

/**
 * @param {number[][]} graph
 * @return {number[][]}
 */
var allPathsSourceTarget = function(graph) {
    const paths = [];
    // Stack stores arrays: [current_node, current_path]
    const stack = [[0, []]]; // Start at node 0 with an empty path
    const targetNode = graph.length - 1;

    while (stack.length > 0) {
        const [node, path] = stack.pop();

        // Create the new path by appending the current node
        const currentPath = [...path, node];

        if (node === targetNode) {
            paths.push(currentPath); // Found a path
            continue;
        }

        // Explore neighbors
        for (const neighbor of graph[node]) {
            stack.push([neighbor, currentPath]); // Push neighbor and the path so far
        }
    }

    return paths;
};

C# #

public class Solution {
    public IList<IList<int>> AllPathsSourceTarget(int[][] graph)
    {
        var paths = new List<IList<int>>();
        // Stack stores tuples: (current_node, current_path)
        var stack = new Stack<(int node, List<int> path)>();
        stack.Push((0, new List<int>())); // Start at node 0

        int targetNode = graph.Length - 1;

        while (stack.Count > 0)
        {
            var (node, path) = stack.Pop();

            var currentPath = new List<int>(path);
            currentPath.Add(node);

            if (node == targetNode)
            {
                paths.Add(currentPath); // Found a path
                continue;
            }

            // Explore neighbors
            foreach (int neighbor in graph[node])
            {
                stack.Push((neighbor, currentPath)); // Push neighbor and the path so far
            }
        }

        return paths;
    }
}

Go #

type StackItem struct {
    Node int
    Path []int
}

func allPathsSourceTarget(graph [][]int) [][]int {
    var paths [][]int
    stack := []StackItem{{Node: 0, Path: []int{}}} // Start at node 0

    targetNode := len(graph) - 1

    for len(stack) > 0 {
        currentItem := stack[len(stack) - 1] // Pop from stack
        stack = stack[:len(stack) - 1]

        node := currentItem.Node
        path := currentItem.Path

        newPath := append([]int(nil), path...)
        newPath = append(newPath, node)

        if node == targetNode {
            paths = append(paths, newPath) // Found a path
            continue
        }

        for _, neighbor := range graph[node] {
            stack = append(stack, StackItem{Node: neighbor, Path: newPath})
        }
    }

    return paths
}

Ruby #

# @param {Integer[][]} graph
# @return {Integer[][]}
def all_paths_source_target(graph)
  paths = []
  # Stack stores arrays: [current_node, current_path]
  stack = [[0, []]] # Start at node 0 with an empty path
  target_node = graph.length - 1

  while !stack.empty?
    node, path = stack.pop

    # Create the new path by appending the current node
    current_path = path + [node]

    if node == target_node
      paths << current_path # Found a path
      next
    end

    # Explore neighbors
    graph[node].each do |neighbor|
      stack.push([neighbor, current_path])
    end
  end

  paths
end

其它语言

欢迎贡献代码到 LeetCode Python GitHub -> 797. 所有可能的路径。感谢！

题解2的思路：用“递归”实现的“深度优先搜索”

“深度优先搜索”的模式

与 BFS 的对比：

搜索顺序：DFS 优先探索深度方向，而广度优先搜索（BFS）按层逐层扩展，形成“先进先出”的队列结构。
适用场景：DFS 更适合强连通分量或回溯类问题（如迷宫所有路径），而 BFS 擅长最短路径（未加权图）或邻近节点探索（如社交网络好友推荐）。

DFS 的独特性：

不完全性：若图无限深或存在环路（未标记已访问），DFS 可能无法终止，而 BFS 总能找到最短路径（未加权图）。
“一支笔走到底” 的搜索风格，使其在回溯剪枝或记录路径时更具灵活性，但也可能错过近邻最优解。

“递归”的模式

递归（Recursion）是计算机科学和数学中的一个重要概念，指的是一个函数在其定义中 直接或间接调用自身 的方法。

递归的核心思想

自我调用：函数在执行过程中调用自身。
基线情况：相当于终止条件。到达基线情况后，就可以返回结果了，不需要再递归调用，防止无限循环。
递归步骤：问题逐步向“基线情况”靠近的步骤。

步骤

初始化一个空数组 paths，用于存储从源节点到目标节点找到的所有有效路径。
定义一个递归深度优先搜索 (DFS) 函数，例如 dfs，它将当前 node 和 path（即迄今为止访问过的节点列表，用于到达当前节点）作为输入。
在 dfs 函数内部：
- 通过将当前 node 附加到 path 来创建一个新的路径列表。我们将其称为 newPath。
- 检查当前 node 是否为目标节点（n - 1，其中 n 是节点总数）。
  - 如果是目标节点，则表示我们找到了一条完整的路径。将 newPath 添加到主 paths 数组中，并从此递归调用返回。
- 如果当前 node 不是目标节点，则遍历所有可从当前 node 访问的 neighbor 节点（即遍历 graph[node]）。
  - 对于每个 neighbor，以 neighbor 作为新的当前节点，以 newPath 作为到达该节点的路径，对 dfs 进行递归调用 (dfs(neighbor, newPath))。
通过使用源节点 0 和空的初始路径 (dfs(0, [])) 调用 dfs 函数来启动该过程。
初始 dfs 调用完成后，返回包含所有已发现路径的 paths 数组。

复杂度

时间复杂度

Too complex

空间复杂度

Too complex

Python #

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        self.paths = []
        self.graph = graph
        self.target = len(graph) - 1

        self.dfs(0, []) # Start DFS from node 0 with an empty initial path

        return self.paths

    def dfs(self, node, path):
        current_path = path + [node]

        if node == self.target: # Base case
            self.paths.append(current_path)
            return

        for neighbor in self.graph[node]: # Recursive step: Explore neighbors
            self.dfs(neighbor, current_path)

Java #

class Solution {
    private List<List<Integer>> paths;
    private int[][] graph;
    private int targetNode;

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        this.paths = new ArrayList<>();
        this.graph = graph;
        this.targetNode = graph.length - 1;

        List<Integer> initialPath = new ArrayList<>();
        dfs(0, initialPath); // Start DFS from node 0 with an empty initial path

        return paths;
    }

    private void dfs(int node, List<Integer> currentPath) {
        List<Integer> newPath = new ArrayList<>(currentPath);
        newPath.add(node);

        if (node == targetNode) { // Base case
            paths.add(newPath);
            return;
        }

        for (int neighbor : graph[node]) { // Recursive step: Explore neighbors
            dfs(neighbor, newPath);
        }
    }
}

C++ #

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        _graph = graph;

        vector<int> initial_path; // Empty initial path
        dfs(0, initial_path); // Start DFS from node 0

        return _paths;
    }

private:
    vector<vector<int>> _paths;
    vector<vector<int>> _graph;

    void dfs(int node, vector<int> current_path) {
        current_path.push_back(node);

        if (node == _graph.size() - 1) { // Base case
            _paths.push_back(current_path);
            return;
        }

        for (int neighbor : _graph[node]) { // Recursive step: Explore neighbors
            dfs(neighbor, current_path);
        }
    }
};

JavaScript #

let paths
let graph

var allPathsSourceTarget = function (graph_) {
  paths = []
  graph = graph_

  dfs(0, [])

  return paths
}

function dfs(node, currentPath) {
  const newPath = [...currentPath, node]

  if (node === graph.length - 1) { // Base case
    paths.push(newPath)
    return
  }

  for (const neighbor of graph[node]) { // Recursive step: Explore neighbors
    dfs(neighbor, newPath)
  }
}

C# #

public class Solution
{
    private IList<IList<int>> paths;
    private int[][] graph;
    private int targetNode;

    public IList<IList<int>> AllPathsSourceTarget(int[][] graph)
    {
        this.paths = new List<IList<int>>();
        this.graph = graph;
        this.targetNode = graph.Length - 1;

        Dfs(0, new List<int>());

        return paths;
    }

    private void Dfs(int node, List<int> currentPath)
    {
        var newPath = new List<int>(currentPath);
        newPath.Add(node);

        if (node == targetNode) // Base case
        {
            paths.Add(newPath);
            return;
        }

        foreach (int neighbor in graph[node]) // Recursive step: Explore neighbors
        {
            Dfs(neighbor, newPath);
        }
    }
}

Go #

var (
    paths [][]int
    graph [][]int
    targetNode int
)

func allPathsSourceTarget(graph_ [][]int) [][]int {
    paths = [][]int{}
    graph = graph_
    targetNode = len(graph) - 1

    dfs(0, []int{})

    return paths
}

func dfs(node int, currentPath []int) {
    newPath := append([]int(nil), currentPath...)
    newPath = append(newPath, node)  

    if node == targetNode { // Base case
        paths = append(paths, newPath)
        return
    }

    for _, neighbor := range graph[node] { // Recursive step: Explore neighbors
        dfs(neighbor, newPath)
    }
}

Ruby #

def all_paths_source_target(graph)
  @paths = []
  @graph = graph

  dfs(0, [])

  @paths
end

def dfs(node, current_path)
  new_path = current_path + [node]

  if node == @graph.size - 1 # Base case
    @paths << new_path
    return
  end

  @graph[node].each do |neighbor| # Recursive step: Explore neighbors
    dfs(neighbor, new_path)
  end
end

其它语言

欢迎贡献代码到 LeetCode Python GitHub -> 797. 所有可能的路径。感谢！

题解3的思路：用“递归”实现的“深度优先搜索”（推荐）

“深度优先搜索”的模式

与 BFS 的对比：

搜索顺序：DFS 优先探索深度方向，而广度优先搜索（BFS）按层逐层扩展，形成“先进先出”的队列结构。
适用场景：DFS 更适合强连通分量或回溯类问题（如迷宫所有路径），而 BFS 擅长最短路径（未加权图）或邻近节点探索（如社交网络好友推荐）。

DFS 的独特性：

不完全性：若图无限深或存在环路（未标记已访问），DFS 可能无法终止，而 BFS 总能找到最短路径（未加权图）。
“一支笔走到底” 的搜索风格，使其在回溯剪枝或记录路径时更具灵活性，但也可能错过近邻最优解。

步骤

初始化一个空列表 paths，用于存储从源节点到目标节点找到的所有有效路径。
创建一个可变列表 path，用于跟踪当前正在探索的路径，初始仅包含源节点 0。
实现一个使用回溯法探索路径的递归 DFS 函数：
- 基线情况：如果当前节点是目标节点 (n-1)，则复制当前路径并将其添加到 paths 列表中。
- 递归步骤：对于当前节点的每个邻居：
  - 将邻居添加到当前路径。
  - 使用此邻居递归调用 DFS 函数。
  - 递归调用返回后，从路径中删除邻居（回溯）。
从源节点 0 开始 DFS。
DFS 完成后，返回收集到的 paths。

复杂度

时间复杂度

Too complex

空间复杂度

Too complex

Python #

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        self.paths = []
        self.graph = graph
        self.path = [0] # Important

        self.dfs(0)

        return self.paths

    def dfs(self, node):
        if node == len(self.graph) - 1:
            self.paths.append(self.path.copy()) # Important
            return

        for neighbor in self.graph[node]:
            self.path.append(neighbor) # Important
            self.dfs(neighbor)
            self.path.pop() # Important

Java #

class Solution {
    private List<List<Integer>> paths = new ArrayList<>();
    private List<Integer> path = new ArrayList<>(List.of(0)); // Important - start with node 0
    private int[][] graph;

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        this.graph = graph;

        dfs(0);

        return paths;
    }

    private void dfs(int node) {
        if (node == graph.length - 1) { // Base case
            paths.add(new ArrayList<>(path)); // Important - make a copy
            return;
        }

        for (int neighbor : graph[node]) { // Recursive step
            path.add(neighbor); // Important
            dfs(neighbor);
            path.remove(path.size() - 1); // Important - backtrack
        }
    }
}

C++ #

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        _graph = graph;
        _path = {0}; // Important - start with node 0

        dfs(0);

        return _paths;
    }

private:
    vector<vector<int>> _paths;
    vector<vector<int>> _graph;
    vector<int> _path;

    void dfs(int node) {
        if (node == _graph.size() - 1) { // Base case
            _paths.push_back(_path); // Important - copy is made automatically
            return;
        }

        for (int neighbor : _graph[node]) { // Recursive step
            _path.push_back(neighbor); // Important
            dfs(neighbor);
            _path.pop_back(); // Important - backtrack
        }
    }
};

JavaScript #

/**
 * @param {number[][]} graph
 * @return {number[][]}
 */
var allPathsSourceTarget = function(graph) {
  const paths = [];
  const path = [0]; // Important - start with node 0

  function dfs(node) {
    if (node === graph.length - 1) { // Base case
      paths.push([...path]); // Important - make a copy
      return;
    }

    for (const neighbor of graph[node]) { // Recursive step
      path.push(neighbor); // Important
      dfs(neighbor);
      path.pop(); // Important - backtrack
    }
  }

  dfs(0);

  return paths;
};

C# #

public class Solution
{
    private IList<IList<int>> paths = new List<IList<int>>();
    private List<int> path = new List<int> { 0 }; // Important - start with node 0
    private int[][] graph;

    public IList<IList<int>> AllPathsSourceTarget(int[][] graph)
    {
        this.graph = graph;

        Dfs(0);

        return paths;
    }

    private void Dfs(int node)
    {
        if (node == graph.Length - 1)
        { // Base case
            paths.Add(new List<int>(path)); // Important - make a copy
            return;
        }

        foreach (int neighbor in graph[node])
        { // Recursive step
            path.Add(neighbor); // Important
            Dfs(neighbor);
            path.RemoveAt(path.Count - 1); // Important - backtrack
        }
    }
}

Go #

func allPathsSourceTarget(graph [][]int) [][]int {
    paths := [][]int{}
    path := []int{0} // Important - start with node 0

    var dfs func(int)
    dfs = func(node int) {
        if node == len(graph) - 1 { // Base case
            // Important - make a deep copy of the path
            paths = append(paths, append([]int(nil), path...))
            return
        }

        for _, neighbor := range graph[node] { // Recursive step
            path = append(path, neighbor) // Important
            dfs(neighbor)
            path = path[:len(path) - 1] // Important - backtrack
        }
    }

    dfs(0)

    return paths
}

Ruby #

# @param {Integer[][]} graph
# @return {Integer[][]}
def all_paths_source_target(graph)
  @paths = []
  @graph = graph
  @path = [0] # Important - start with node 0

  dfs(0)

  @paths
end

def dfs(node)
  if node == @graph.length - 1 # Base case
    @paths << @path.clone # Important - make a copy
    return
  end

  @graph[node].each do |neighbor| # Recursive step
    @path << neighbor # Important
    dfs(neighbor)
    @path.pop # Important - backtrack
  end
end

其它语言

欢迎贡献代码到 LeetCode Python GitHub -> 797. 所有可能的路径。感谢！

上一题下一题

游客

全部题解

Welcome !

LeetCode Python, Java, C++ > 图论 > 797. 所有可能的路径 > 已支持 Python, Java, C++, JavaScript, C#, Go, Ruby > LeetCode GitHub Code 或 转发

示例 1:

示例 2:

约束:

思路 上一题下一题

“深度优先搜索”的模式

步骤

复杂度

时间复杂度

空间复杂度

Python #

Java #

C++ #

JavaScript #

C# #

Go #

Ruby #

其它语言

题解2的思路：用“递归”实现的“深度优先搜索”

“深度优先搜索”的模式

“递归”的模式

递归的核心思想

步骤

复杂度

时间复杂度

空间复杂度

Python #

Java #

C++ #

JavaScript #

C# #

Go #

Ruby #

其它语言

题解3的思路：用“递归”实现的“深度优先搜索”（推荐）

“深度优先搜索”的模式

步骤

复杂度

时间复杂度

空间复杂度

Python #

Java #

C++ #

JavaScript #

C# #

Go #

Ruby #

其它语言

LeetCode Python, Java, C++ > 图论 > 797. 所有可能的路径 > 已支持 Python, Java, C++, JavaScript, C#, Go, Ruby > LeetCode GitHub Code 或转发

思路
上一题下一题