797. All Paths From Source to Target - Solved in Python/Java/C++/JavaScript/C#/Go/Ruby

LeetCode Python/Java/C++/JS > Graph Theory > 797. All Paths From Source to Target > Solved in Python, Java, C++, JavaScript, C#, Go, Ruby > LeetCode GitHub Code or Repost

LeetCode link: 797. All Paths From Source to Target, difficulty: Medium.

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Example 1:

Input: graph = [[1,2],[3],[3],[]]

Output: [[0,1,3],[0,2,3]]

Explanation:

There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:

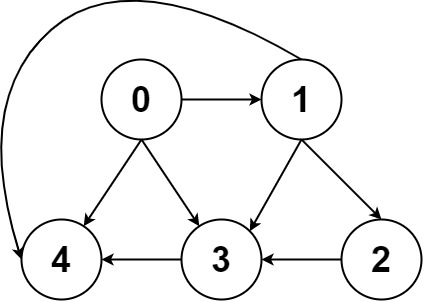
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]

Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

Constraints:

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i (i.e., there will be no self-loops).
All the elements of graph[i] are unique.
The input graph is guaranteed to be a DAG.

Intuition
Previous Next

Pattern of "Depth-First Search"

Depth-First Search (DFS) is a classic graph traversal algorithm characterized by its "go as deep as possible" approach when exploring branches of a graph. Starting from the initial vertex, DFS follows a single path as far as possible until it reaches a vertex with no unvisited adjacent nodes, then backtracks to the nearest branching point to continue exploration. This process is implemented using recursion or an explicit stack (iterative method), resulting in a Last-In-First-Out (LIFO) search order. As a result, DFS can quickly reach deep-level nodes far from the starting point in unweighted graphs.

Comparison with BFS:

Search Order: DFS prioritizes depth-wise exploration, while Breadth-First Search (BFS) expands layer by layer, following a First-In-First-Out (FIFO) queue structure.
Use Cases: DFS is better suited for strongly connected components or backtracking problems (e.g., finding all paths in a maze), whereas BFS excels at finding the shortest path (in unweighted graphs) or exploring neighboring nodes (e.g., friend recommendations in social networks).

Unique Aspects of DFS:

Incompleteness: If the graph is infinitely deep or contains cycles (without visited markers), DFS may fail to terminate, whereas BFS always finds the shortest path (in unweighted graphs).
"One-path deep-dive" search style makes it more flexible for backtracking, pruning, or path recording, but it may also miss near-optimal solutions.

In summary, DFS reveals the vertical structure of a graph through its depth-first strategy. Its inherent backtracking mechanism, combined with the natural use of a stack, makes it highly effective for path recording and state-space exploration. However, precautions must be taken to handle cycles and the potential absence of optimal solutions.

Step by Step Solutions

Initialize an empty list paths to store all valid paths found.
Initialize a stack to manage the DFS traversal. Each element on the stack will store a pair (or tuple) containing the current node and the path taken to reach that node.
Push the starting state onto the stack: the initial node 0 and an empty path list (e.g., (0, [])).
While the stack is not empty:
- Pop the top element from the stack, retrieving the current node and its associated path.
- Create a currentPath list by appending the current node to the path popped from the stack. This represents the path leading up to and including the current node.
- Check if the current node is the target node (n - 1, where n is the total number of nodes).
  - If it is the target node, add the currentPath to the paths list, as a complete path from source to target has been found.
  - If it is not the target node, iterate through all neighbor nodes accessible from the current node (i.e., iterate through graph[node]).
    - For each neighbor, push a new pair onto the stack: the neighbor node and the currentPath. This prepares the traversal to explore paths extending from the neighbor.
After the loop finishes (stack is empty), return the paths list containing all discovered paths from node 0 to node n - 1.

Complexity

Time complexity

Too complex

Space complexity

Too complex

Python #

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        paths = []
        stack = [(0, [])]

        while stack:
            node, path = stack.pop()

            if node == len(graph) - 1:
                paths.append(path + [node])
                continue

            for target_node in graph[node]:
                stack.append((target_node, path + [node]))

        return paths

Java #

class Solution {
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        List<List<Integer>> paths = new ArrayList<>();
        // Each element in the stack is a pair: (current_node, current_path)
        Stack<Pair<Integer, List<Integer>>> stack = new Stack<>();
        List<Integer> initialPath = new ArrayList<>();
        stack.push(new Pair<>(0, initialPath));

        int targetNode = graph.length - 1;

        while (!stack.isEmpty()) {
            var current = stack.pop();
            int node = current.getKey();
            var path = current.getValue();

            var nextPath = new ArrayList<>(path);
            nextPath.add(node);

            if (node == targetNode) {
                paths.add(nextPath);
                continue;
            }

            for (int neighbor : graph[node]) {
                stack.push(new Pair<>(neighbor, nextPath));
            }
        }

        return paths;
    }
}

C++ #

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        vector<vector<int>> paths;
        // Stack stores pairs of (current_node, current_path)
        stack<pair<int, vector<int>>> s;
        s.push({0, {}}); // Start at node 0 with an empty path initially

        int targetNode = graph.size() - 1;

        while (!s.empty()) {
            auto node_path = s.top();
            s.pop();
            int node = node_path.first;
            vector<int> path = node_path.second;

            // Add the current node to the path
            path.push_back(node);

            if (node == targetNode) {
                paths.push_back(path); // Found a path to the target
                continue;
            }

            // Explore neighbors
            for (int neighbor : graph[node]) {
                s.push({neighbor, path});
            }
        }

        return paths;
    }
};

JavaScript #

/**
 * @param {number[][]} graph
 * @return {number[][]}
 */
var allPathsSourceTarget = function(graph) {
    const paths = [];
    // Stack stores arrays: [current_node, current_path]
    const stack = [[0, []]]; // Start at node 0 with an empty path
    const targetNode = graph.length - 1;

    while (stack.length > 0) {
        const [node, path] = stack.pop();

        // Create the new path by appending the current node
        const currentPath = [...path, node];

        if (node === targetNode) {
            paths.push(currentPath); // Found a path
            continue;
        }

        // Explore neighbors
        for (const neighbor of graph[node]) {
            stack.push([neighbor, currentPath]); // Push neighbor and the path so far
        }
    }

    return paths;
};

C# #

public class Solution {
    public IList<IList<int>> AllPathsSourceTarget(int[][] graph)
    {
        var paths = new List<IList<int>>();
        // Stack stores tuples: (current_node, current_path)
        var stack = new Stack<(int node, List<int> path)>();
        stack.Push((0, new List<int>())); // Start at node 0

        int targetNode = graph.Length - 1;

        while (stack.Count > 0)
        {
            var (node, path) = stack.Pop();

            var currentPath = new List<int>(path);
            currentPath.Add(node);

            if (node == targetNode)
            {
                paths.Add(currentPath); // Found a path
                continue;
            }

            // Explore neighbors
            foreach (int neighbor in graph[node])
            {
                stack.Push((neighbor, currentPath)); // Push neighbor and the path so far
            }
        }

        return paths;
    }
}

Go #

type StackItem struct {
    Node int
    Path []int
}

func allPathsSourceTarget(graph [][]int) [][]int {
    var paths [][]int
    stack := []StackItem{{Node: 0, Path: []int{}}} // Start at node 0

    targetNode := len(graph) - 1

    for len(stack) > 0 {
        currentItem := stack[len(stack) - 1] // Pop from stack
        stack = stack[:len(stack) - 1]

        node := currentItem.Node
        path := currentItem.Path

        newPath := append([]int(nil), path...)
        newPath = append(newPath, node)

        if node == targetNode {
            paths = append(paths, newPath) // Found a path
            continue
        }

        for _, neighbor := range graph[node] {
            stack = append(stack, StackItem{Node: neighbor, Path: newPath})
        }
    }

    return paths
}

Ruby #

# @param {Integer[][]} graph
# @return {Integer[][]}
def all_paths_source_target(graph)
  paths = []
  # Stack stores arrays: [current_node, current_path]
  stack = [[0, []]] # Start at node 0 with an empty path
  target_node = graph.length - 1

  while !stack.empty?
    node, path = stack.pop

    # Create the new path by appending the current node
    current_path = path + [node]

    if node == target_node
      paths << current_path # Found a path
      next
    end

    # Explore neighbors
    graph[node].each do |neighbor|
      stack.push([neighbor, current_path])
    end
  end

  paths
end

Other languages

Welcome to contribute code to LeetCode Python GitHub -> 797. All Paths From Source to Target. Thanks!

Intuition of solution 2: "Depth-First Search" by Recursion

Pattern of "Depth-First Search"

Comparison with BFS:

Search Order: DFS prioritizes depth-wise exploration, while Breadth-First Search (BFS) expands layer by layer, following a First-In-First-Out (FIFO) queue structure.
Use Cases: DFS is better suited for strongly connected components or backtracking problems (e.g., finding all paths in a maze), whereas BFS excels at finding the shortest path (in unweighted graphs) or exploring neighboring nodes (e.g., friend recommendations in social networks).

Unique Aspects of DFS:

Incompleteness: If the graph is infinitely deep or contains cycles (without visited markers), DFS may fail to terminate, whereas BFS always finds the shortest path (in unweighted graphs).
"One-path deep-dive" search style makes it more flexible for backtracking, pruning, or path recording, but it may also miss near-optimal solutions.

Pattern of "Recursion"

Recursion is an important concept in computer science and mathematics, which refers to the method by which a function calls itself directly or indirectly in its definition.

The core idea of recursion

Self-call: A function calls itself during execution.
Base case: Equivalent to the termination condition. After reaching the base case, the result can be returned without recursive calls to prevent infinite loops.
Recursive step: The step by which the problem gradually approaches the "base case".

Step by Step Solutions

Initialize an empty list paths to store all the valid paths found from source to target.
Define a recursive Depth-First Search (DFS) function, say dfs, that takes the current node and the currentPath (a list of nodes visited so far to reach the current node) as input.
Inside the dfs function: a. Create a new path list by appending the current node to the currentPath. Let's call this newPath. b. Check if the current node is the target node (n - 1, where n is the total number of nodes). i. If it is the target node, it means we've found a complete path. Add newPath to the main paths list and return from this recursive call. c. If the current node is not the target node, iterate through all neighbor nodes accessible from the current node (i.e., iterate through graph[node]). i. For each neighbor, make a recursive call to dfs with the neighbor as the new current node and newPath as the path taken to reach it (dfs(neighbor, newPath)).
Start the process by calling the dfs function with the source node 0 and an empty initial path (dfs(0, [])).
After the initial dfs call completes, return the paths list containing all discovered paths.

Complexity

Time complexity

Too complex

Space complexity

Too complex

Python #

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        self.paths = []
        self.graph = graph
        self.target = len(graph) - 1

        self.dfs(0, []) # Start DFS from node 0 with an empty initial path

        return self.paths

    def dfs(self, node, path):
        current_path = path + [node]

        if node == self.target: # Base case
            self.paths.append(current_path)
            return

        for neighbor in self.graph[node]: # Recursive step: Explore neighbors
            self.dfs(neighbor, current_path)

Java #

class Solution {
    private List<List<Integer>> paths;
    private int[][] graph;
    private int targetNode;

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        this.paths = new ArrayList<>();
        this.graph = graph;
        this.targetNode = graph.length - 1;

        List<Integer> initialPath = new ArrayList<>();
        dfs(0, initialPath); // Start DFS from node 0 with an empty initial path

        return paths;
    }

    private void dfs(int node, List<Integer> currentPath) {
        List<Integer> newPath = new ArrayList<>(currentPath);
        newPath.add(node);

        if (node == targetNode) { // Base case
            paths.add(newPath);
            return;
        }

        for (int neighbor : graph[node]) { // Recursive step: Explore neighbors
            dfs(neighbor, newPath);
        }
    }
}

C++ #

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        _graph = graph;

        vector<int> initial_path; // Empty initial path
        dfs(0, initial_path); // Start DFS from node 0

        return _paths;
    }

private:
    vector<vector<int>> _paths;
    vector<vector<int>> _graph;

    void dfs(int node, vector<int> current_path) {
        current_path.push_back(node);

        if (node == _graph.size() - 1) { // Base case
            _paths.push_back(current_path);
            return;
        }

        for (int neighbor : _graph[node]) { // Recursive step: Explore neighbors
            dfs(neighbor, current_path);
        }
    }
};

JavaScript #

let paths
let graph

var allPathsSourceTarget = function (graph_) {
  paths = []
  graph = graph_

  dfs(0, [])

  return paths
}

function dfs(node, currentPath) {
  const newPath = [...currentPath, node]

  if (node === graph.length - 1) { // Base case
    paths.push(newPath)
    return
  }

  for (const neighbor of graph[node]) { // Recursive step: Explore neighbors
    dfs(neighbor, newPath)
  }
}

C# #

public class Solution
{
    private IList<IList<int>> paths;
    private int[][] graph;
    private int targetNode;

    public IList<IList<int>> AllPathsSourceTarget(int[][] graph)
    {
        this.paths = new List<IList<int>>();
        this.graph = graph;
        this.targetNode = graph.Length - 1;

        Dfs(0, new List<int>());

        return paths;
    }

    private void Dfs(int node, List<int> currentPath)
    {
        var newPath = new List<int>(currentPath);
        newPath.Add(node);

        if (node == targetNode) // Base case
        {
            paths.Add(newPath);
            return;
        }

        foreach (int neighbor in graph[node]) // Recursive step: Explore neighbors
        {
            Dfs(neighbor, newPath);
        }
    }
}

Go #

var (
    paths [][]int
    graph [][]int
    targetNode int
)

func allPathsSourceTarget(graph_ [][]int) [][]int {
    paths = [][]int{}
    graph = graph_
    targetNode = len(graph) - 1

    dfs(0, []int{})

    return paths
}

func dfs(node int, currentPath []int) {
    newPath := append([]int(nil), currentPath...)
    newPath = append(newPath, node)  

    if node == targetNode { // Base case
        paths = append(paths, newPath)
        return
    }

    for _, neighbor := range graph[node] { // Recursive step: Explore neighbors
        dfs(neighbor, newPath)
    }
}

Ruby #

def all_paths_source_target(graph)
  @paths = []
  @graph = graph

  dfs(0, [])

  @paths
end

def dfs(node, current_path)
  new_path = current_path + [node]

  if node == @graph.size - 1 # Base case
    @paths << new_path
    return
  end

  @graph[node].each do |neighbor| # Recursive step: Explore neighbors
    dfs(neighbor, new_path)
  end
end

Other languages

Welcome to contribute code to LeetCode Python GitHub -> 797. All Paths From Source to Target. Thanks!

Intuition of solution 3: DFS by Recursion (Recommended)

Pattern of "Depth-First Search"

Comparison with BFS:

Search Order: DFS prioritizes depth-wise exploration, while Breadth-First Search (BFS) expands layer by layer, following a First-In-First-Out (FIFO) queue structure.
Use Cases: DFS is better suited for strongly connected components or backtracking problems (e.g., finding all paths in a maze), whereas BFS excels at finding the shortest path (in unweighted graphs) or exploring neighboring nodes (e.g., friend recommendations in social networks).

Unique Aspects of DFS:

Incompleteness: If the graph is infinitely deep or contains cycles (without visited markers), DFS may fail to terminate, whereas BFS always finds the shortest path (in unweighted graphs).
"One-path deep-dive" search style makes it more flexible for backtracking, pruning, or path recording, but it may also miss near-optimal solutions.

Step by Step Solutions

Initialize an empty list paths to store all valid paths found from the source to the target.
Create a mutable list path to track the current path being explored, initially containing only the source node 0.
Implement a recursive DFS function that explores paths using backtracking:
- Base case: If the current node is the target node (n-1), make a copy of the current path and add it to the paths list.
- Recursive step: For each neighbor of the current node:
  - Add the neighbor to the current path.
  - Recursively call the DFS function with this neighbor.
  - After the recursive call returns, remove the neighbor from the path (backtrack).
Start the DFS from the source node 0.
Return the collected paths after the DFS completes.

Complexity

Time complexity

Too complex

Space complexity

Too complex

Python #

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        self.paths = []
        self.graph = graph
        self.path = [0] # Important

        self.dfs(0)

        return self.paths

    def dfs(self, node):
        if node == len(self.graph) - 1:
            self.paths.append(self.path.copy()) # Important
            return

        for neighbor in self.graph[node]:
            self.path.append(neighbor) # Important
            self.dfs(neighbor)
            self.path.pop() # Important

Java #

class Solution {
    private List<List<Integer>> paths = new ArrayList<>();
    private List<Integer> path = new ArrayList<>(List.of(0)); // Important - start with node 0
    private int[][] graph;

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        this.graph = graph;

        dfs(0);

        return paths;
    }

    private void dfs(int node) {
        if (node == graph.length - 1) { // Base case
            paths.add(new ArrayList<>(path)); // Important - make a copy
            return;
        }

        for (int neighbor : graph[node]) { // Recursive step
            path.add(neighbor); // Important
            dfs(neighbor);
            path.remove(path.size() - 1); // Important - backtrack
        }
    }
}

C++ #

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        _graph = graph;
        _path = {0}; // Important - start with node 0

        dfs(0);

        return _paths;
    }

private:
    vector<vector<int>> _paths;
    vector<vector<int>> _graph;
    vector<int> _path;

    void dfs(int node) {
        if (node == _graph.size() - 1) { // Base case
            _paths.push_back(_path); // Important - copy is made automatically
            return;
        }

        for (int neighbor : _graph[node]) { // Recursive step
            _path.push_back(neighbor); // Important
            dfs(neighbor);
            _path.pop_back(); // Important - backtrack
        }
    }
};

JavaScript #

/**
 * @param {number[][]} graph
 * @return {number[][]}
 */
var allPathsSourceTarget = function(graph) {
  const paths = [];
  const path = [0]; // Important - start with node 0

  function dfs(node) {
    if (node === graph.length - 1) { // Base case
      paths.push([...path]); // Important - make a copy
      return;
    }

    for (const neighbor of graph[node]) { // Recursive step
      path.push(neighbor); // Important
      dfs(neighbor);
      path.pop(); // Important - backtrack
    }
  }

  dfs(0);

  return paths;
};

C# #

public class Solution
{
    private IList<IList<int>> paths = new List<IList<int>>();
    private List<int> path = new List<int> { 0 }; // Important - start with node 0
    private int[][] graph;

    public IList<IList<int>> AllPathsSourceTarget(int[][] graph)
    {
        this.graph = graph;

        Dfs(0);

        return paths;
    }

    private void Dfs(int node)
    {
        if (node == graph.Length - 1)
        { // Base case
            paths.Add(new List<int>(path)); // Important - make a copy
            return;
        }

        foreach (int neighbor in graph[node])
        { // Recursive step
            path.Add(neighbor); // Important
            Dfs(neighbor);
            path.RemoveAt(path.Count - 1); // Important - backtrack
        }
    }
}

Go #

func allPathsSourceTarget(graph [][]int) [][]int {
    paths := [][]int{}
    path := []int{0} // Important - start with node 0

    var dfs func(int)
    dfs = func(node int) {
        if node == len(graph) - 1 { // Base case
            // Important - make a deep copy of the path
            paths = append(paths, append([]int(nil), path...))
            return
        }

        for _, neighbor := range graph[node] { // Recursive step
            path = append(path, neighbor) // Important
            dfs(neighbor)
            path = path[:len(path) - 1] // Important - backtrack
        }
    }

    dfs(0)

    return paths
}

Ruby #

# @param {Integer[][]} graph
# @return {Integer[][]}
def all_paths_source_target(graph)
  @paths = []
  @graph = graph
  @path = [0] # Important - start with node 0

  dfs(0)

  @paths
end

def dfs(node)
  if node == @graph.length - 1 # Base case
    @paths << @path.clone # Important - make a copy
    return
  end

  @graph[node].each do |neighbor| # Recursive step
    @path << neighbor # Important
    dfs(neighbor)
    @path.pop # Important - backtrack
  end
end

Other languages

Welcome to contribute code to LeetCode Python GitHub -> 797. All Paths From Source to Target. Thanks!

Previous Next

Unregistered user

All solutions

Welcome !

LeetCode Python/Java/C++/JS > Graph Theory > 797. All Paths From Source to Target > Solved in Python, Java, C++, JavaScript, C#, Go, Ruby > LeetCode GitHub Code or Repost

Example 1:

Example 2:

Constraints:

Intuition PreviousNext

Pattern of "Depth-First Search"

Step by Step Solutions

Complexity

Time complexity

Space complexity

Python #

Java #

C++ #

JavaScript #

C# #

Go #

Ruby #

Other languages

Intuition of solution 2: "Depth-First Search" by Recursion

Pattern of "Depth-First Search"

Pattern of "Recursion"

The core idea of ​​recursion

Step by Step Solutions

Complexity

Time complexity

Space complexity

Python #

Java #

C++ #

JavaScript #

C# #

Go #

Ruby #

Other languages

Intuition of solution 3: DFS by Recursion (Recommended)

Pattern of "Depth-First Search"

Step by Step Solutions

Complexity

Time complexity

Space complexity

Python #

Java #

C++ #

JavaScript #

C# #

Go #

Ruby #

Other languages

Intuition
Previous Next

The core idea of recursion